Bem hoje vamos falar da notação Big O, matemática e código, tudo que um desenvolvedor gostar, correto? (Ouvi um sim daqui). Mas, calma, antes de tudo vamos alinhar as expectativas, até porque, combinado não sai caro, nesse artigo irei falar sobre o que é a notação, porque usá-la.
Chega de enrolação, e vamos para uma breve explicação abaixo:
Na matemática, a notação Big-O descreve o comportamento limitante de uma função quando o argumento tende a um valor específico ou para o infinito, normalmente, em termos de funções mais simples. É membro de uma família maior de notações conhecida como notação Landau, notação Bachmann–Landau ou notação assintótica.
- Grande-O – Wikipédia, a enciclopédia livre (wikipedia.org)
Essa definição causa mais dúvida do que entendimento, mas como dizia o filosofo Jason, vamos por partes, primeiro quando se fala em limitante imagine duas funções, f(x) e g(x), onde existe dois eixos (x, y) em um plano cartesiano, onde y representa o esforço que um programa realiza ao executar em relação a x que é a entrada a ser processada, quando digo que a função f(x) é limitante superior a g(x) estou falando que g(x) nunca vai ter um valor maior em y dado a mesma entrada x.
No caso do Big O a ideia é saber qual é o limite superior, essa forma de analisar, conhecida também por “pior caso” referente ao comportamento do esforço em relação ao dado que irá ser processado, vai possibilitar entender o comportamento e medir a eficiência do seu código. Parece errôneo pensar sempre no pior caso, mas segue uma frase de exemplo “Meu salário como Analista de TI não é maior que o salário do melhor jogador de futebol do Brasil”, acredito que ficaram na dúvida, mas é verdade a afirmação acima, porém não é uma declaração precisa, mesmo assim não deixa de ser verdadeira.
Então vamos para um exemplo teórico, O(n), chamada de função linear ou de primeiro grau, A letra n representa o tamanho da entrada, quanto a função f(n) = n interna ao O() nós dá ideia da complexidade do algoritmo em função da entrada, considerando que a complexidade interfere no comportamento de crescimento do esforço de execução, logo quanto maior a função, maior vai ser o esforço, e com isso você terá noção se seu código teria um selo tipo A no inmetro (Aquele selo que vem quando você compra algum produto eletrônico por exemplo).
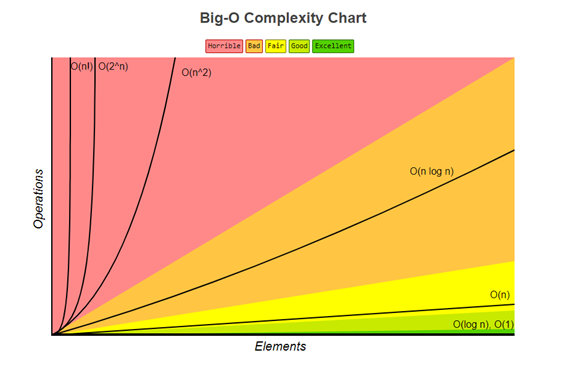
Imagem com a lista de complexidade, fonte https://www.bigocheatsheet.com/
A imagem acima segue exemplo do comportamento de funções, a ideia e ter sempre algoritmos na faixa verde para amarelo, nem sempre isso vai ser possível. Recomendo inclusive acessar o site https://www.bigocheatsheet.com/ lá vocês encontraram complexidade de estruturas de dados conhecidas e a complexidade das operações. Voltando para exemplos anteriores o eixo Elements pode considerar a entrada(s) e o Operations o tempo de retorno dado o número de operações necessárias, fica nítido que um O(n) função constante irá processar em um tempo menor ou igual a função O(n²) função quadrática dado a mesma entrada n.
Um ponto importante, para a complexidade não importa a função em si, mas sim a ordem de grandeza, imagine uma função f(x) = x² + 100x, a notação dessa função f(x) seria O(x²), função quadrática, por se tratar de uma função polinomial, e ter uma parte como função quadrática e outra função linear, escolhemos a de maior grandeza para representar.
Bem, espero que tenham gostado, no próximo irei demostrar como realizar o calculo de complexidade e falar sobre algoritmos conhecidos, até lá.